Question 4
a) Given Boolean Function F(A,B,C,D) = π(0,1,2,3,5,7,8,9,10,11)
i) Reduce the above expression using 4-variable Karnaugh Map , showing the various groups (i.e. octal , quad and pair) [4]
ii) Draw the logic gate diagram for the reduced expression . Assume that the variables and the complements are available as inputs. [1]
Sol i)
From the above Karnaugh Map we get a octet (M0M1M2M3M8M9M10M11 ) that gives reduced expression : B
The quad (M1M3M5M7) gives expression :A+D'
Therefore, the reduced expression for the Boolean Function is B.(A+D')
ii)
b) Given Boolean Function
P(A,B,C,D)= ABC'D'+ A'BC'D' + A'BC'D + ABC'D+A'BCD + ABCD
i) Reduce the above expression using 4-variable Karnaugh Map , showing the various groups (i.e. octal , quad and pair) [4]
ii) Draw the logic gate diagram for the reduced expression . Assume that the variables and the complements are available as inputs. [1]
Sol i)
From the first quad ( m4m5m12m13) we get : BC'
From the second quad (m5m7m13m15)we get : BD
Therefore the reduced expression of the above Boolean Sum of Products expression is : BC'+BD
ii)
Question 5.
A person is allowed to travel on a reserved coach on train , if he/she satisfies the criteria below
(In all the above cases 1 indicates YES and 0 indicates NO.)
Output : T - Denotes allowed to travel. 1 indicates YES and 0 indicates NO
a) Draw the truth table for the inputs and outputs given . Write the POS expression for T(R,P,D,H). [5]
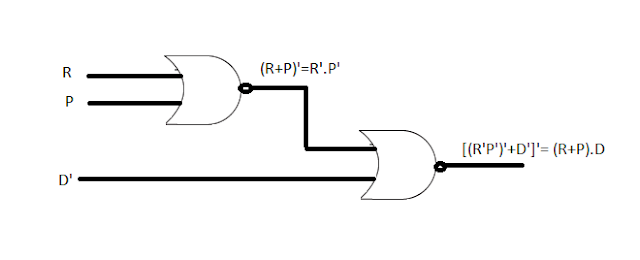
b) Reduce T(R,P,D,H) using Karnaugh map. Draw the logic gate diagram for the reduced POS using only NOR gates
assuming that the variables and their complements are allowed as inputs. [5]
Sol,
a)
The POS expression for the above truth table is :
T(R,P,D,H) = π(0,1,2,3,4,5,8,9,12,13)
From the octal (M0M1M4M5M8M9M12M13) : D
Therefore , the reduced POS of T(R,P,D,H) = (R+P).D
Question 6.
a) Draw the truth table and logic diagram for an octal to binary encoder. [4]
Sol.
b) What is Multiplexer? State an application of Multiplexer. Also, draw the logic diagram of 4:1 Multiplexer. [4]
c) Verify the following expression using Boolean Laws. Also, mention the laws used at each step of simplification.
X.Y.Z+X.Y'.Z+X.Y.Z' = X.(Y+Z) [2]
Sol.
L.H.S.= X.Y.Z+X.Y'.Z+X.Y.Z'
=X.Y.Z+X.Y.Z'+X.Y'.Z
=X.Y.(Z+Z') + X.Y'.Z
= X.Y+ X.Y'.Z (Since by Complementary Law Z+Z'=1)
=X.(Y+Y'Z)
=X.(Y+Y')(Y+Z) (Since by Distributive Law A+B.C=(A+B).(A+C))
=X.(Y+Z) (Since by Complementary Law Y+Y'=1)
= R.H.S.
Question 7:
a) Derive a Boolean expression for the logic circuit given below and reduce the derived expression using Boolean Laws. [3]
[Note : You are to solve any three questions from this part . As I have mentioned in a post earlier , it is better to attempt the two questions on Karnaugh Map . Question No 6 involves truth tables , diagrams that are quite time consuming . Question 4 is pretty straight as expected. Question 5 is easy, only you have to be patient while computing the truth table. Questions 7b and 7c are again nothing tricky . Attempt 7a step by step . Write the output for each gate on the diagram of your question paper and you are good to go .]
a) Given Boolean Function F(A,B,C,D) = π(0,1,2,3,5,7,8,9,10,11)
i) Reduce the above expression using 4-variable Karnaugh Map , showing the various groups (i.e. octal , quad and pair) [4]
ii) Draw the logic gate diagram for the reduced expression . Assume that the variables and the complements are available as inputs. [1]
Sol i)
From the above Karnaugh Map we get a octet (M0M1M2M3M8M9M10M11 ) that gives reduced expression : B
The quad (M1M3M5M7) gives expression :A+D'
Therefore, the reduced expression for the Boolean Function is B.(A+D')
ii)
b) Given Boolean Function
P(A,B,C,D)= ABC'D'+ A'BC'D' + A'BC'D + ABC'D+A'BCD + ABCD
i) Reduce the above expression using 4-variable Karnaugh Map , showing the various groups (i.e. octal , quad and pair) [4]
ii) Draw the logic gate diagram for the reduced expression . Assume that the variables and the complements are available as inputs. [1]
Sol i)
From the first quad ( m4m5m12m13) we get : BC'
From the second quad (m5m7m13m15)we get : BD
Therefore the reduced expression of the above Boolean Sum of Products expression is : BC'+BD
ii)
Question 5.
A person is allowed to travel on a reserved coach on train , if he/she satisfies the criteria below
- Person has a valid reservation ticket and a valid ID proof OR
- The person does not have a valid reservation ticket , but holds a valid pass issued by Railway department with a valid ID proof. OR
- The person is disabled and holds a valid pass issued by the Railway department along with a valid ID proof.
Input
|
|
R
|
Person has valid reservation ticket
|
P
|
Person holds a valid pass from Railway Department
|
D
|
Person has a valid ID proof
|
H
|
Person is disabled
|
R
|
P
|
D
|
H
|
T
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
b)
From the octal (M0M1M4M5M8M9M12M13) : D
Therefore , the reduced POS of T(R,P,D,H) = (R+P).D
Question 6.
a) Draw the truth table and logic diagram for an octal to binary encoder. [4]
Sol.
Octal No.
|
Truth
Table
|
Output
|
|||||||||
D0
|
D1
|
D2
|
D3
|
D4
|
D5
|
D6
|
D7
|
a
|
b
|
c
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
2
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
3
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
4
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
5
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
6
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
7
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
Sol.
A multiplexer is a combinational circuit that selects binary information from one or many lines and directs it to a single output line.
It is used for bandwidth utilization so finds it's application in data transmission , routing of signal , telephone exchange.
The Logic circuit is as follows;
X.Y.Z+X.Y'.Z+X.Y.Z' = X.(Y+Z) [2]
Sol.
L.H.S.= X.Y.Z+X.Y'.Z+X.Y.Z'
=X.Y.Z+X.Y.Z'+X.Y'.Z
=X.Y.(Z+Z') + X.Y'.Z
= X.Y+ X.Y'.Z (Since by Complementary Law Z+Z'=1)
=X.(Y+Y'Z)
=X.(Y+Y')(Y+Z) (Since by Distributive Law A+B.C=(A+B).(A+C))
=X.(Y+Z) (Since by Complementary Law Y+Y'=1)
= R.H.S.
Question 7:
a) Derive a Boolean expression for the logic circuit given below and reduce the derived expression using Boolean Laws. [3]
Sol.
1. A'
2. B'
3. C'
4. A'.B'.C'
5 (A'.B'.C')'
6. (A'.B'.C')'.C
7. X = (A'.B'.C')'.C+(A'.B'.C')'
(A'.B'.C')'.C+(A'.B'.C')'
=( A+B+C).C+(A+B+C)
= A.C+B.C+C.C+A+B+C
= A.C+B.C+C+A+B+C
=(A.C+A) +( B.C+ B) + C
=A+B+C
b) What are universal gates ? Construct a logic circuit using NAND gates only for expression A.(B+C) . [4]
Sol. When any digital system can be implemented by a logic gate , the gate is said to be universal . Eg : NAND gates .
c) Define Half Adders. Draw circuit diagram and truth table for a Half Adder . [4]
Sol,
c) Half Adder is an example of a simple functional digital circuit built from two logic gates . The half adder adds two one-bit binary numbers (A, B) . The output is the sum of two bits (S) and the carry (C). The truth table of the half adder is as follows
The logic diagram of half adder is given below,












No comments:
Post a Comment